Nanotechnology Blog | thoughts and ideas on nanotechnology

Analog & Digital – Part II

Posted on October 31, 2023 by Walt | Permalink 0

Today’s electronics are based on the transistor, which can be switched either on (a one) or off (a zero). Among other things, the sounds coming from musical instruments are basically smooth variations, which are described as analog signals. In order for the signals (electronic representations of the sound waves) to be processed, there must be a conversion from the analog wave to a digital representation of the original wave. An analog to digital converter continuously transforms analog signals into the binary (ones and zeros) equivalent at each instant of measurement that can be processed by the electronic equipment.

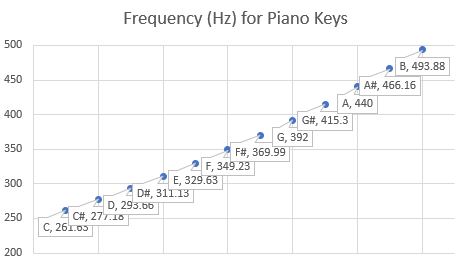
Consider the piano and violin representation of their frequencies between C and B (twelve notes) on a piano. Figure 1 shows the 12 notes from C through B, with the A being the key frequency of 440 Hz. [Re. 1] The point of this chart is to present the fact that the piano has fixed notes and is more like digital information from a computer. The violin, on the other hand would provide a continuous range of the various frequencies. (There is also a slight variation of the piano key frequencies from a straight line for the violin.)

Figure 1

One interesting item is that since the piano has discrete frequencies associated with the various keys, the actual sound is not a smooth ramp up and down like a sine wave.

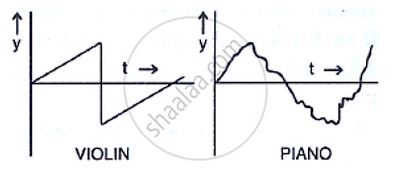
Figure Two depicts a violin and a piano note and shows the rapid drop-off of the note from the violin. [Ref. 2]

Figure 2

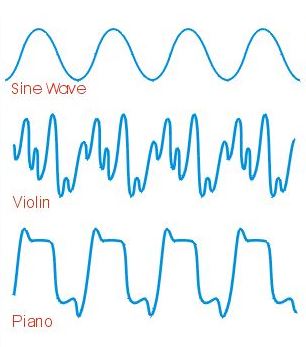
The piano note is created by the key striking the stretched piano wire that has been properly tuned. The initial strike is full of non-harmonic tones that dampen down rapidly. [Ref. 3] This reverberation from the strike produces the wave form. The violin is different in that the vibrating string creates harmonics that create the multitude of peaks and valleys shown in Figure 3 [Ref. 4].

Figure 3

I will borrow some explanation of harmonics from reference 5. It explains that the instrument produces different wave shapes based on the shape of the instrument. that demonstrate comparison of wave shape and harmonics. Another factor is the way the note is played. “If you press a piano key and release it, the sound changes volume gradually over time. First, it rises quickly (or “attacks”) to its maximum volume. Next, the sound “decays” to a lower level and stays there or “sustains.” Finally, when we let go of the key, the sound “releases” and dies down to silence.”

” There are other factors too. An instrument doesn’t just produce a single sound wave at a single pitch (frequency). Even if it’s playing a steady note, it’s making many different sound waves at once: it makes one note (called a fundamental frequency or first harmonic) and lots of higher, related notes called harmonics or overtones. The frequency of each harmonic is a multiple of the fundamental frequency. So, if the fundamental frequency (also called the first harmonic) is 200Hz (which we can think of as simply 1 × 200Hz), the second harmonic is 400Hz (2 × 200Hz), the third is 600Hz (3 × 200Hz), the fourth is 800Hz (4 × 200Hz), and so on. Playing together, the harmonics make a dense, complex sound a bit like a barber’s shop choir, with low voices and high voices all singing in tune. The more harmonics there are, the richer the sound.”

Getting back to Analog and Digital, what the instrument is delivering is a continues series of complex waves that include small and smaller portions of the waves. Taking these waves and “chopping” them up into discrete segments has to average out the variation in each of the measurement size chunks of sound waves. So, no matter how fine one dissects the wave, there is averaging with each bite-sized piece of the actual music. It is possible to take that measurement down to a small enough size that the typical listener will not notice the subtle differences from the analog. BUT, sound can also be subtly felt. No matter how small the averaging size, there will be a difference from the original analog sound wave. Consequently, vinyl (records) is making a come back due to the superior reproduction of actual sounds due to vinyl being an analog delivery of the sounds.

References:

Technology

Analog & Digital – Part I

Posted on September 30, 2023 by Walt | Permalink 0

There is no question that we live in a digital world. What does that mean? Is there another world? What is the difference? We live in a world of computers. Computers are based on components of electrical circuits. The basic part of the circuit is defined by either being “on” (conducting electrical signals) or “off” (not conducting). Each of these basic circuit parts in considered a “bit”. So, a 32 bit controller divides the control in to 32 steps, while a 64 bit has 64 steps. Notice, the term “steps”. If one considers a child’s slide, it is a continuous slope. If we were to make that digital, it would have small steps in place of the continuous slide. We would not do that, of course. But we do that with electronics. Have you ever tried to adjust the volume from a speaker and found one setting was too much and next lower setting was too little? That is due to the digital steps in the controller. It is possible to increase the steps to make it appear to be smooth, but it would still be steps.

From Reference 1: “An analog computer or analogue computer is a type of computer that uses the continuous variation aspect of physical phenomena such as electrical, mechanical, or hydraulic quantities (analog signals) to model the problem being solved. In contrast, digital computers represent varying quantities symbolically and by discrete values of both time and amplitude (digital signals).” Analog computers were used in the 1940 to provide assistance with fire control weapons systems during World War II among other applications.

The digital computer became the standard for multiple reasons. The speed of calculation became greater and greater than analog computers. There was one fundamental issue that hindered the application of analog computers. Reprogramming was accomplished by rearranging the interconnecting wires/cables within the assembly. Digital computers in the early days had basic system instructions (neumonic identifiers) that were entered into the computer via numerical codes. This was slow but faster than rewiring the system. When the operating systems emerged for digital computers, the computer could perform a multitude of tasks and not be designed for specific problems.

If digital is faster (and better?) than analog, why are people going back to vinyl records? Why do these people state that the quality of the music is better? Vinyl records are made by equipment that records the actual frequencies as analog signals into to a master copy that captures the nuances of the changes in frequencies. This implies that the equipment can record the analog signals, which implies a system with vacuum tubes and not computer-generated analog to digital converters. To obtain the true effect of the music to be similar to being at and actual performance (not amplified by digital equipment) requires the equipment playing the sounds is also capable of producing analog signals with out electronic digital to analog conversion.

In a very crude example. A piano key strikes a chord that vibrates at a given frequency. The key next to it is at a known, discrete frequency. E.g., the middle C of a piano is 261.6 HZ, the black key to the right has a frequency of 277.18 Hz. This is not continuous as it would be for an instrument like a violin. The piano is the digital instrument (discrete bits) and the violin is the analog (continuous frequencies). The recording in Reference 2 was done during a practice session by “eg” and has both piano and violin music. The quality of the recording is not very good, but the differences between the piano (digital) sound and the violin (analog) sounds are obvious. This example was recorded in an auditorium with a small voice recorder, which was digital. The point is there is a recognizable difference between the analog and digital type sounds.

Next month, Part II will delve into some of the subtleties of employing digitally modified analog signal along with more on sound itself. The modification does not come without consequences.

References:

Technology

Power Challenges for Greater Computing

Posted on August 31, 2023 by Walt | Permalink 0

As mentioned in previous blogs [Ref. 1] the power consumption to manufacture semiconductors has raised concern. The International Roadmap for Devices and Systems (IRDS) [Ref. 2] has been evaluating that issue. There is no short-term solution as the complexity of the circuitry continues to increase. Changes that are being evaluated, e.g., chiplets, do not reduce the demand for semiconductor devices, but are options to produce and yield devices more efficiently.

Reference 3 provides an interesting view into alternate power sources for high performance devices. The article indicates that high-end CPUs can require as much as 700W per chip. As shown in the chart in June 2023 blog, the power consumption is trending to be beyond the requirements to obtain enough power to satisfy the demand. As pointed out, architectures at 7nm and below require lower operating voltages, which creates a need for higher currents. The problem with the power delivery networks PDNs) is that they must be able to maintain a constant power supply under conditions that can be very rapidly changing. One solution is to change the IT infrastructure from 12 volts to 48 volts.

What difference does this make? For the same power, the current at 48 volts is ¼ the current required at 12 volts. The power loss is defined by I²R. So, reducing the current by a factor of 4 reduces the power loss by a factor of 16. Reference 3, provides an example of a 10MW data center that would save 1.4 million kWh per year. Not considering the cost saving, the reduction in the power consumption can help lower the projected power consumption in the country. To make this happen requires a change in most of the large computing centers equipment.

This in not addressing the power required to run the Artificial Intelligence processors. Reference 4 states: “It’s unclear exactly how much energy is needed to run the world’s AI models. One data scientist trying to tackle the question ended up with an estimate that ChatGPT’s electricity consumption was between 1.1M and 23M KWh in January 2023 alone. There’s a lot of room between 1.1 million and 23 million, but it’s safe to say AI requires an obtuse and immense amount of energy. Incorporating large language models into search engines could mean up to a fivefold increase in computing power. Some even warn machine learning is on track to consume all energy being supplied.”

There was an interesting comparison at the end of the reference 4 article: “A computer can play Go and even beat humans,” said McClelland. “But it will take a computer something like100 kilowatts to do so while our brains do it for just 20watts.”

“The brain is an obvious place to look for a better way to compute AI.”

So will we continue to make larger and larger models or will we find better solutions? Is it time to rethink the standard semiconductor architecture? Part of this is being pursued through the development of chiplets, which can permit placing memory closer to the processor that needs the memory. That would cut down on the circuitry wiring the signal needs to traverse. In turn, that should reduce the power consumption and speed up the computing process. With new materials being developed, new potential applications should be possible. The future always has a way of surprising us. We shall see what happens next.

References:

April, May, and June 2023 blogs
https://irds.ieee.org/editions
https://www.eetimes.com/the-challenges-of-powering-big-ai-chips/
https://blog.westerndigital.com/solving-ai-power-problem/

Semiconductor Technology

More Optical Metamaterials

Posted on July 31, 2023 by Walt | Permalink 0

Previous blogs have covered metamaterials for optics including an invisibility cloak. Reference 1 moves into the shorter wavelengths of extreme ultraviolet (EUV) light. It is interesting in that the original work waw focused on attosecond physics. (atto is 10^-18) This field of physics is working to understand physical processes like photoelectric effect by creating short pulses of EUV. The image area they were working on was to incorporate a single focal point of 10mm. They were using 50nm EUV light. The final design consisted of a 200nm film etched wit million holes. The key accomplishment is they produced a membrane for 50nm EUV light that behaves like a lens with optical light. Current semiconductor EUV lithography is in the 12nm wavelength range and uses reflective optics. This is not a simple transition to take the existing work and make it into semiconductor masks. But, it shows that it is possible to use metamaterials to focus wavelengths that we currently do not have a good method for achieving the results. This is not a complete project for semiconscious. The researchers indicated the fabrication of this metalens required creating images that were five time smaller than they have previously done to create the focal point. Semiconductors would require a further reduction by a factor of four and be able to design structures that have multiple type of structure images.

An article [Ref. 2] in the July 2023 issue of IEEE Spectrum magazine addressed the challenges in today’s shrinking cameras that exist in phones and many other products. It points out that the most space-consuming part of the camera is the lens. It is typically a difficult trade off. A shorter focal length (small distance to the imaging device) requires a thick center part of the lens (more thickness equals more space). This does not consider that stronger curved create aberrations that distort the different wavelengths of the image, which require additional optics. SO the solution was to replace conventional optical technology with a new technology – the metalens. The metalens is manufactured using semiconductor processing technology to create structures a few hundred microns thick. The article employs an example of a shallow marsh with grass standing in water. The grass moves with the incoming water and changes the position of the grass. Then different height grass would have different effect on the overall picture due to the motion of each individual stalk of grass. The following is directly from the article [Ref. 2]:

“The objects in the scene bounce the light all over the place. Some of this light comes back toward the metalens, which is pointed, pillars out, toward the scene. These returning photons hit the tops of the pillars and transfer their energy into vibrations. The vibrations—called plasmons—travel down the pillars. When that energy reaches the bottom of a pillar, it exits as photons, which can be then captured by an image sensor. Those photons don’t need to have the same properties as those that entered the pillars; we can change these properties by the way we design and distribute the pillars.”

The design incorporates both height and thickness of the ”stalks” to change the characteristic of the incoming energy. There is always more work to create finer structures and more precise heights. However, the metalens is an engineered material construct that can provide wave control functions previously unavailable.

References:

Metamaterials, Semiconductor Technology

The Issue with Artificial Intelligence (AI)

Posted on June 30, 2023 by Walt | Permalink 0

The issue of AI has been in the headlines of major newspapers with all kinds of doom projections. Reference 1 from earlier this year has 11 areas that should create worry. These items include replacing humans a variety of jobs resulting in significant reductions in the work force. The one that is appropriate in today’s concerns in the impact on the environment.

AI can provide a help in establishing low emission infrastructure and other related efforts that can be assisted by increased algorithms that provide a better understanding of the activities impacting the environment. This sounds good, but, as with most things, there is a catch.

The training required for advanced AI models, quality data takes computing power to obtain and process. Employing the results to train a significant focused model requires energy consumption. Reference 2 has examples of training data size for models. OpenAI trained it GPT-3 on 45 terabytes if data. Microsoft trained a smaller system (less data) using 512 Nvidia GPU for nine days. The power consumption was 27,648 watts or enough energy to power 3 homes for a year. This was for a smaller model than GPT-3.

As the capabilities of the models increase the amount of data grows exponentially. Reference 3 has a graph, Figure 1, projects the Machine Learning systems will be pushing its total of the world power supply. The question of why the energy demand is growing so quickly is that more accurate models require more data. More accurate models generate more profitability.

There is another issue. The available semiconductor processing capability is a limiting factor. Therefore, more wafer fabs are required, which fabs in themselves, area a power consumption concern. The storage clouds are not exempt from this increase in power requirements. Reference 4 indicates that the power consumption of the computer racks in the storage center require 4 times as much power as a tradition CPU rack. There is work being done in this area to reduce the power requirements, but that reduction is being outstripped by the increase in data being processed.

What is the difference between the CPU and GPU racks that increase the power consumption? A CPU (Central Processing Unit) is the main controller for all the circuitry. It covers a variety of processes and runs processes serially with a number of cores that does not currently exceed 64. Most desktops have less than 12 cores. This unit is efficient at processing one task at a time. The GPU (Graphical Processing Unit) is specially designed to handle many smaller processes at a time, like graphics or video rendering. The core count is in the thousands to run processes in parallel.

This provides the specialized GPU with the ability to have a heavy load of processing without having to be concerned with the other tasks the computer needs to do. So, the circuitry does not include the capability of day-to-day operations, but has extra computational power directed at specific circuits.

The net result is that faster processing employs more power. That power must be generated somewhere. That increase in electricity generation raises concerns about the total impact on the environment. This is where AI becomes an environmental concern.

References:

Science, Technology

3-D and Electronics

Posted on May 31, 2023 by Walt | Permalink 0

There has been a lot written about 2-D transistors and the coming applications involving the properties of the circuitry and its ability to create denser circuitry. There are challenges as the circuit density increases. While very small, the distance that an electrical signal needs to travel reduces the effective speed of the processor. So, one solution is to place small pieces of memory near the processor circuitry. It is also possible to place small amounts of specialized circuitry near other resources required by that circuitry.

Let’s consider the issues as stand-alone problems, which they are not. If one considers chiplets, there is the problem of aligning the chiplet with the circuitry that it is being attached to. Since the line widths are on the order of low digit nanometers alignment is critical. The methodology for blind alignment would require high precision on the dimensions of the chiplet. One solution would be to thin the wafer so that the circuitry being mounted is transparent and can be accurately aligned. While this may seem unreasonable, thinning wafers to below 30 µm changes the transmission of light through the wafer so that alignment can be done with a great deal of accuracy. Next, let’s consider attachment. Since the circuitry is being miniaturized the available space for bonding pads becomes much smaller. So, the question that comes up is how much is the minimum amount of area that is required to guarantee a connection which does not change under temperature loading. Work is being done in this area, but there is no agreed upon direction at this time. Even when these problems are sufficiently solved to permit manufacturing, the question comes up how to inspect the joints/connections of the two pieces of circuitry. Visual inspection is highly improbable since even thinned wafers would have circuit minds on the substrate that blocked the ability to visually inspect. Solving this problem then raises another question. The current design of semiconductors is such that the bottom of the semiconductors can be mounted tightly to a heat transfer material. This permits the ability to cool the devices that are generating heat and take that heat away from the circuit. High temperatures over long periods of time tend to degrade the performance of the circuitry. If one considers the stacked circuits, the upper portions of the stack circuit do not have the thermal conductivity that would exist if it were a single level of circuitry. That raises the question of what is the heat contribution to these upper-level devices and will it cause early failure. This needs to be addressed, and people are working on it. However, we don’t have the solution in hand yet. So, 3-D circuitry has potential but there are many issues that need to be addressed.

One area that 3-D had provided some promise is the attempt to print batteries onto circuits. Back in 2016, there were proposals to employ a 3-D holographic lithography to create these batteries [Ref. 1]. The limiting factor is the 3-D creation of thee required electrode formation. There are current claims regarding the development of 3-D printed batteries [Ref. 2], but the public release has been slow.

3-D electronics has potential to improve the existing products, but there is still much research and development required.

References:

Electronics, Semiconductor Technology, Uncategorized

Artificial Intelligence (AI) and Nano Technology

Posted on April 30, 2023 by Walt | Permalink 0

“AI” has become a “hot” topic in both technical publications and general newspapers. There have been multiple stories of ChatGPT 3.5 and 4.0 and other Chatbots [Ref 1]. The addition of AI to search engines by Google (BARD) and Microsoft’s Bing (ChatGPT+) [Ref. 2]. Browsers, like Chrome, have been adding AI capable features [Ref. 3]. The has been news from the medical field of AI being employed by medical professionals and improving the diagnosis of patients [Ref. 4]. On the negative side, there was a publication about Chaos-GPT with very negative connotations [Ref. 5]. How do these chatbots apply to nano technology, or does the technology even apply?

There have been many attempts to produce tools that can assist humans in making decisions or even make the decisions itself. Automation of equipment is an obvious example. In the lumber industry, equipment has been developed that inspects a segment of a harvested tree, calculates the orientation to get the maximum lumber from the tree, and then does the actual cutting [Ref. 6]. The ongoing work for self-driving vehicles is another application of AI. The millions of lines of code keep increasing as new options have to be allowed depending on the circumstances that the vehicle is encountering.

ChatGPT was developed by OpenAI as a chatbot [Ref. 7] and is different from previously released chatbots. While it was released in November of 2022, it was not until later March 2023 that its applications started making headlines because the responses did not require accessing a restricted set of data, but permitted unstructured assembling on the response data to random questions in a manner and format that provides the appearance of a knowledgeable response. Algorithms are developed to guide the collection and organization of data relevant to the subject under investigation. A proper arrangement of algorithms can make it appear as being answered by a person.

In the 1980s, there was significant work on expert systems, which are a precursor to today’s algorithm driven chatbots. Computing power and the cost of storage were orders of magnitude less capable than today. The amount of data available was significantly less and the speed of the computations were much slower. Still there were interesting developments. One of the observations from that work was that each expert system had to have a starting base of data. As the system encountered additional data of choices and the outcomes, the database changed the probabilities of the possible outcomes. So, the system “evolved” based on its environment, i.e. machine learning. A system for farming in colder climes would provide different answers from one in the tropics. Understandable, due to the two systems being distinct.

Today’s computing power is orders of magnitude greater than the early 1990s. The memory capacity has also increased greatly. But so has the data. It the author’s opinion that there is more data created and stored on line in a single day now than there was in an entire year in the 1990s. This raises the question of where will and how will the chatbots get their information. One of the recent reviews indicated that it is possible that some chatbots have information that was current in 2018. A lot happens in five years.

A recent article [Ref. 8] express the concerns of an AI ethicist. The development of machine-learning algorithms to assist in the responses of a chatbot could lead to replacing judgement on situations with the chatbots’ output. She is quoted as saying “Using chatbots in search engines . . . is a bonkers idea that everyone is now racing to do to.”

It is too early to decide how the machine learning chatbots will evolve and assist in developing new materials or technologies in the nano realm. In the late 1990s, Text Mining was the next computer driven technology that would provide a very widespread application. It has evolved to applications that are focused, e.g., evaluating customer databases to determine produce or service issues or similar evaluation of structured word evaluation. A report from Stanford states: “A lot of inefficiencies and errors that happen in medicine today occur because of the hyper-specialization of human doctors and the slow and spotty flow of information” [Ref. 9]. Hopefully, nanotechnology will witness something that can evaluate research similarities and provide a database as appears to be happening in medicine that researchers nano realm can utilize to move toward the future more quickly. Chatbots can apply to nanotechnology given the proper access to relevant data.

References:

Top 25 Chatbot Case Studies & Success Stories in 2023 https://research.aimultiple.com/top-chatbot-success/
https://www.pcmag.com/news/chatgpt-alternatives-ai-chatbots-ready-to-answer-your-burning-questions
https://www.digitaltrends.com/computing/best-ai-chatbots/
The AI Will See You Now, Wall Street Journal, Saturday, 04/08/2023 Page .C001
https://decrypt.co/126122/meet-chaos-gpt-ai-tool-destroy-humanity
https://www.innovating-automation.blog/why-a-sawmill-needs-automation/
Https://chatgpt.pro
Weekend Confidential with Timnit Gebru, Emily Bobrow, Wall Street journal, Saturday, 02/25/2023 Page .C006
https://news.stanford.edu/press-releases/2023/04/12/advances-generalizable-medical-ai/

Technology

New transistors in the nano realm

Posted on March 31, 2023 by Walt | Permalink 0

The current structures for semiconductor central processing units (CPUs) are being designed and produced with some dimensions in the single digit nanometer realm. Beside being hard to make, there are material challenges. When one wants to build a structure, whether it is a large building of a very small line, the roughness (irregularities) in the edges are an issue. Bricks can be off a little with respect to each other and still create the appearance of a straight line. But, if there were large stones on a small wall, the appearance would be very obvious. As the size of the lines and objects get smaller and smaller, the molecules that create the structure can be large enough to irregularities in the structure, which can create issues with the electrical properties of the devices.

Smaller structures would appear to be able to be created faster and with less energy. If the structures need to be more precise in alignment and reduction in irregularities, fast exposures might not be the best approach. There are variations in the energy beams doing the exposure. Everything needs to be uniform. One method is to increase the energy required to form the image of the structure, which means making the imaging material less sensitive. This requires a balance of image structure formation and overall throughput of the equipment, which implies greater energy needed for manufacturing. This raises the possibility of needing new materials and new structures.

Reference 1 is from a business and technology guru, George Gilder. He mentions that Huawei has patented a graphene transistor. (Other companies have patented different ideas and structures.) He states: “Huawei’s breakthrough is deeply impressive. Because graphene is a supreme conductor of both heat and electricity, graphene transistors may operate at 10 times, or more, the speed of silicon devices, using perhaps less than a tenth of the power. . . graphene conducts electrons with minimal resistance and graphene transistors need far less power than silicon to switch on and off. But they will be slow no longer, switching at least an order of magnitude faster than silicon. And as a “two dimensional” (i.e., one atom thick) material graphene circuits could function with only atomic distances between them.”

There is continuing development in the area of metamaterials. Engineers from CalTech and ETH Zurich created a method to design metamaterials using quantum mechanics principles. [Ref. 2] Work has been done on bending electromagnetic waves. An earlier set of blogs have described the impact of metamaterials designed for specific purposes. This team approached the design of metamaterials based on quantum theory. The researchers realized that “quantum mechanics predicts the existence of certain exotic types of matter: among them, a ‘topological insulator’ that conducts electricity across its surface while acting as an insulator in its interior. They realized that they could build macro-scale versions of these exotic systems that could conduct and insulate against vibrations instead of electricity by using principles of quantum mechanics.”

Given that it is possible to create metamaterials , how does this relate to semiconductors. As mentioned, creating means of focusing and bending light, open the possibility of creating optical connections in the semiconductor device. Optical waves can move faster than the electrons. This creates increased speed and a lower energy level, which means less energy loss , which would have become heat. So, it would be faster and use less power. What about the transistor itself? With the ability to create metamaterials that function in very different ways, the design tools are coming that could provide the ability to design a new functioning “transistor”. It still needs to be invented. Coming soon?

References:

1. https://www.gilderreport.com/when-we-have-to-beg-the-chinese-for-their-technology-will-the-china-hawks-lead-the-delegation/

2. https://www.sciencedaily.com/releases/2018/01/180118100819.htm

Electronics, Metamaterials, Nanotechnology

More nanomaterials, or is it metamaterials, or semiconductors?

Posted on February 28, 2023 by Walt | Permalink 0

Last month’s blog covered changes that are coming in the structure of semiconductor transistors. With the announcement of 3nm devices [Ref. 1}, there is no uncertainty that the structures are being designed in the small nanoscale region. As this shrinkage continues, the application of 2 dimensional materials (2-D) is increasingly important.

Energy efficiency of devices is important in order to continue miniaturization of devices and provide improved performance. A devices, like phones, add more functions in roughly the same form shape and size, the ability to have longer battery life (more power for a longer time) is more important. This same ability is key for creating electric vehicles (EVs) with increased travel range. Solutions are developed, but the process sometimes can take a long time.

A paper [Ref. 2] in 2015 describes work started in 2011 on improved layering methods to produce 2-D materials with interesting properties. Work has been focused on transition metal dicho9cogenides. This examines the properties of the combination of one of the 15 transition metals (Molybdenum, Tungsten, etc.) with one of the chalcogen family (sulfur, selenium, and tellurium). At that time, there were hopes to develop a combination that could be employed in place of silicon. The work in 2015 expanded the original possibilities by sandwiching a transition metal, like titanium, between monoatomic layers of another metal and employ carbon atoms to bind the layers together and produce a stable material. The key to their success is the discovery of a material called MAX phase. (M is for the transition Metal, A is for “A group” metals, and the X is for carbon and/or nitrogen.) This terminology was based on material developed in 2011 and called “MXene”, which is based on the process of etching and exfoliating atomically thin layers of aluminum from MAX phases.

Figure 1 is from the authors paper [Ref. 3] showing the detailed structure of the MXenes.

“Schematics of the new MXene structures. (a) Currently available MXenes, where M can be Ti, V, Nb, Ta, forming either monatomic M layers or intermixing between two different M elements to make solid solutions. (b) Discovering the new families of double transition metals MXenes, with two structures as M′2M″C2 and M′2M″2C3, adds more than 20 new MXene carbides, in which the surface M′ atoms can be different from the inner M″ atoms. M′ and M″ atoms can be Ti, V, Nb, Ta, Cr, Mo. (c) Each MXene can have at least three different surface termination groups (OH, O, and F), adding to the variety of the newly discovered MXenes”. [Ref. 3]

Fast forward to 2023, a report [Ref. 4] describes the anticipated advantages of the MXenes in a number of potential applications. MXenes are produced as nanometer thick flakes, which can be dispersed in water or other solution and applied to surfaces. Work has been done to create a supercapacitor and apply it to fabric. The material has been demonstrated to be able to power a 6-volt device for over an hour. While this seems promising as a replacement of lithium-ion batteries, there are issues. The MXenes tend to oxide and degrade in normal conditions. A solution has been demonstrated employing high frequency acoustic waves to remove the rust. It is a fast process that is repeatable. The contention is that the MXenes created for this purpose have four times the storage density of Lithium-ion batteries.

Additional work on employing MXenes, with characteristics favorable to sensors, for medical purposes, such as detecting cancer. Combining the MXenes with a gold nanoarray provided a base for in -situ testing. Adding specific biosensors for identifying specific biomarkers has been demonstrated. This is an early effort to improve detection of specific cancers. There is much research still required to develop this as a usable device.

While there has been a number of promising applications, the immediate availability is not happening. One of the reasons is that there is no source for a consistent supply of the material. The challenge will be to develop processes that provide consistent high-grade material. Until then, MXenes are a great material for developing materials that could have breakthrough results.

References:

Metamaterials, Nanotechnology, Semiconductor Technology

A New Year, New Opportunities

Posted on January 31, 2023 by Walt | Permalink 0

Semiconductors are always in the news as the drive for greater capabilities in ever decreasing package sizes. With the announcement of 3nm node devices going into production, the challenges continue to increase. TSMC has started a pilot production of 3nm devices [Ref. 1]. The shrinkage in size is at the point where there are needs for new transistor designs. The direction appears to be moving from FinFET to a Gate-All-Around FETs design. Figure 1 is from reference 2.

Obviously, there are manufacturing challenges. One of the proposed GAA FET designs is based on nanosheets of material. It appears that some manufactures will introduce the nanosheet FET at 3nm and others at 2nm. (More details on the development of the FETs can be found in reference 2.)

Research at Tsinghua University in Beijing, China have developed a transistor with atomically thinned channels that have a gate length of 0.34nm. [Ref. 3 & 4] This is still years from manufacturing possibilities if it happens at all. Multiple technologies are developed, but a very limited number are able to be developed where the process would work in volume manufacturing. However, this work indicates there a possibilities for continued reduction in the size of the transistors.

Researchers at Georgia Tech, Tianjin University, and Kwansei Gakuin University have demonstrated a nanoelectronics platform based on graphene [Ref. 5]. The process employs e-beam lithography to connect the edges to silicon carbide devices. If oxygen can connect to the graphene, it becomes graphane, which is an insulator.

There are other options for improving the performance capabilities of the semiconductor devices. Chiplets [Ref. 6] are small elements of a circuit that can be employed across a large variety of devices. The advantages of chiplets include the ability of co-locating processors with memory immediately adjacent. This reduces the time it takes a signal to move to or from memory, which results in improved performance. But, nothing is without challenges. Reference 7 covers the need for heterogeneous integration to create multi-die packages. The advantage of smaller area die/chips provides the ability to increase yields due to less complex individual semiconductor functions.

There is another consideration when stacking chiplets. A single semiconductor die is built into a package that dissipates heat to keep the device temperature from becoming too hot. Stacking one or more chiplets removes these portions of the circuitry away from a heat sync. The buildup of heat will impact performance and could have an adverse impact on long-term device reliability.

All of the efforts within the semiconductor industry and researchers worldwide has coordination. In the 1990s, the International Technology Roadmap for Semiconductors (ITRS) was developed to provide guidance for researchers to address future needs that would be required to be in production over the next 10 to 15 years. This roadmap was updated annually. The roadmap committee restructured the ITRS format to address seven different technology areas. The roadmap was renamed the International Roadmap for Devices and Systems (IRDS) to more appropriately address the needs of the complete process. The responsibility of the IRDS was moved from the roadmap committee to the Institute of Electrical and Electronic Engineers (IEEE). The focus of the IRDS is still the requirements for the next fifteen years on a continually moving basis. More details and the roadmap are available is reference 8.

Changes are coming to semiconductor technology that will improve the performance of devices and create new opportunities for innovate products that require greater computing power.

References:

Semiconductor Technology

Archives

Meta